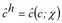Alle Komponenten der dynamischen Gleichgewichtsumlegung wurden vorgestellt. Hier wird das Nutzergleichgewicht, bei dem kein Nutzer seine empfundenen Kosten durch das einseitige Wechseln von Wegen reduzieren kann, als Fixpunktproblem in den Ganglinien der Kantenzuflüsse und -abflüsse beschrieben.
Der deterministische Ansatz
Aus dem Ansatz der impliziten Wegeaufzählung ergibt sich das in Abbildung 132 dargestellte Modell.
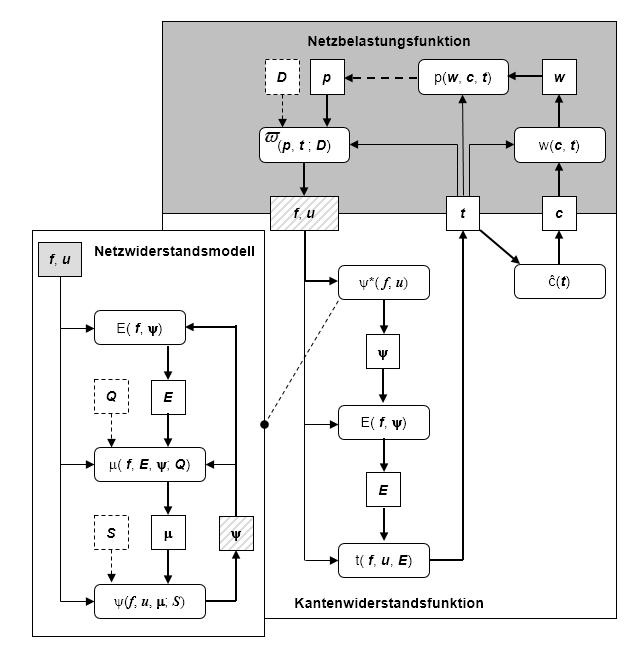
Abbildung 132: Variablen und Modelle der Fixpunktansätze für das Netzwiderstandsmodell (linke Seite) und für die dynamische Umlegung mit Rückstau (rechte Seite)
Analog zum statischen Fall ist die Netzbelastungsfunktion eine Abbildung, die für eine bestimmte Nachfrage D die Kantenbelastung f in Übereinstimmung mit den Kantenreisezeiten und -kosten t und c aus dem deterministischen Routenwahlmodell p(w(c, t), t, c) und dem Flusspropagierungsmodell ω (p, t; D) bestimmt. Die Umlegung benutzt eine implizite Wegeaufzählung und basiert auf den minimalen Kosten w von jedem Knoten zum Ziel sowie auf den daraus resultierenden bedingten Wahrscheinlichkeiten p der Kanten. Das Kantenwiderstandsmodell erzeugt wiederum die Kantenabflusszeiten t und die Kantenkosten c passend zu den Kantenzuflüssen f und den Kantenabflüssen u. Das deterministische Nutzergleichgewicht ergibt sich durch Rückkopplung von Netzbelastungsfunktion und Kantenwiderstandsmodell.
Der Probit-Ansatz
Im Probit-Routenwahlmodell, das auf der Random Utility Theory beruht, sind die von den Nutzer*innen empfundenen Kantenkosten nicht exakt bekannt und gelten daher als unabhängige Zufallsvariablen. Das Probit-Modell für statische Umlegungen wird dynamisiert, indem davon ausgegangen wird, dass die von Nutzer*innen zum Zeitpunkt t empfundenen Kantenkosten ĉa(τ) der Kante a∈A der Summe aus den Kantenkosten ca(τ) des Kantenwiderstandsmodells und einem zeitlich veränderlichen Zufallsfehler entsprechen, dessen Wert zum Zeitpunkt t normalverteilt ist. Wir setzen voraus, dass dessen Varianz proportional zu einem zeitlich veränderlichen Kostenterm χa(τ) > 0 und unabhängig vom Belastungszustand ist.
Die Kantenbelastungen, die aus der Auswertung der Probit-NLM für bestimmte Kantenwiderstände resultieren, werden wie folgt mit der bekannten Montecarlo-Methode bestimmt.
1. H empfundene Kantenkosten werden wie folgt zufällig gezogen.
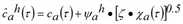
In kompakter Form ergibt sich
Dabei stammt jedes Ψa(τ) aus einer Standard-Normal-Verteilung N[0,1], h = 1, … , H.
2. Für jede Ziehung wird mit der deterministischen NLM ein konsistenter Kantenzufluss bestimmt.
3. Der aus den deterministischen Kantenzuflüssen resultierende Mittelwert wird berechnet, woraus sich eine unverzerrte Schätzung des Probit-Kantenzuflusses ergibt.
Gemäß Gleichung [59] wird die gesamte Ganglinie ĉah(τ) mit einer einzigen Zufallszahl gestört, das heißt der Schätzfehler der Verkehrsteilnehmer ist unabhängig von der Tageszeit. Dies stimmt mit dem Verhalten von Nutzer*innen überein, die die Kantenkostenganglinie ganzheitlich wahrnehmen. Die Fahrzeiten, die der Flusspropagierung zu Grunde liegen, werden hingegen während der Simulation nicht gestört.